
对【树】的大概认识
树的定义
【百度百科上是这样说的】
树,木本植物之总名,主要由根、干、枝、叶、花、果组成。 
树是一种数据结构,它是由个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
- 每个结点有零个或多个子结点;
- 没有父结点的结点称为根结点;
- 每一个非根结点有且只有一个父结点;
- 除了根结点外,每个子结点可以分为多个不相交的子树
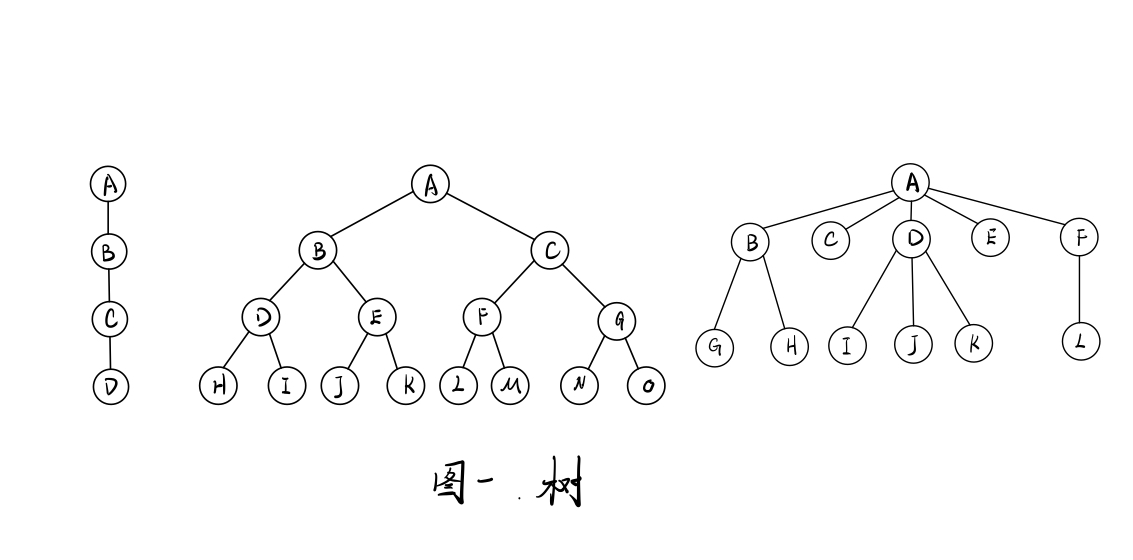
树的种类
- 无序树:树中任意节点的子结点之间没有顺序关系,这种树称为无序树,也称为自由树【说人话就是一棵还没有确定谁是根的树,再说的直白点就是一个没有回路的连通图】
- 有序树:树中任意节点的子结点之间有顺序关系,这种树称为有序树
- 二叉树:每个节点最多含有两个子树的树称为二叉树
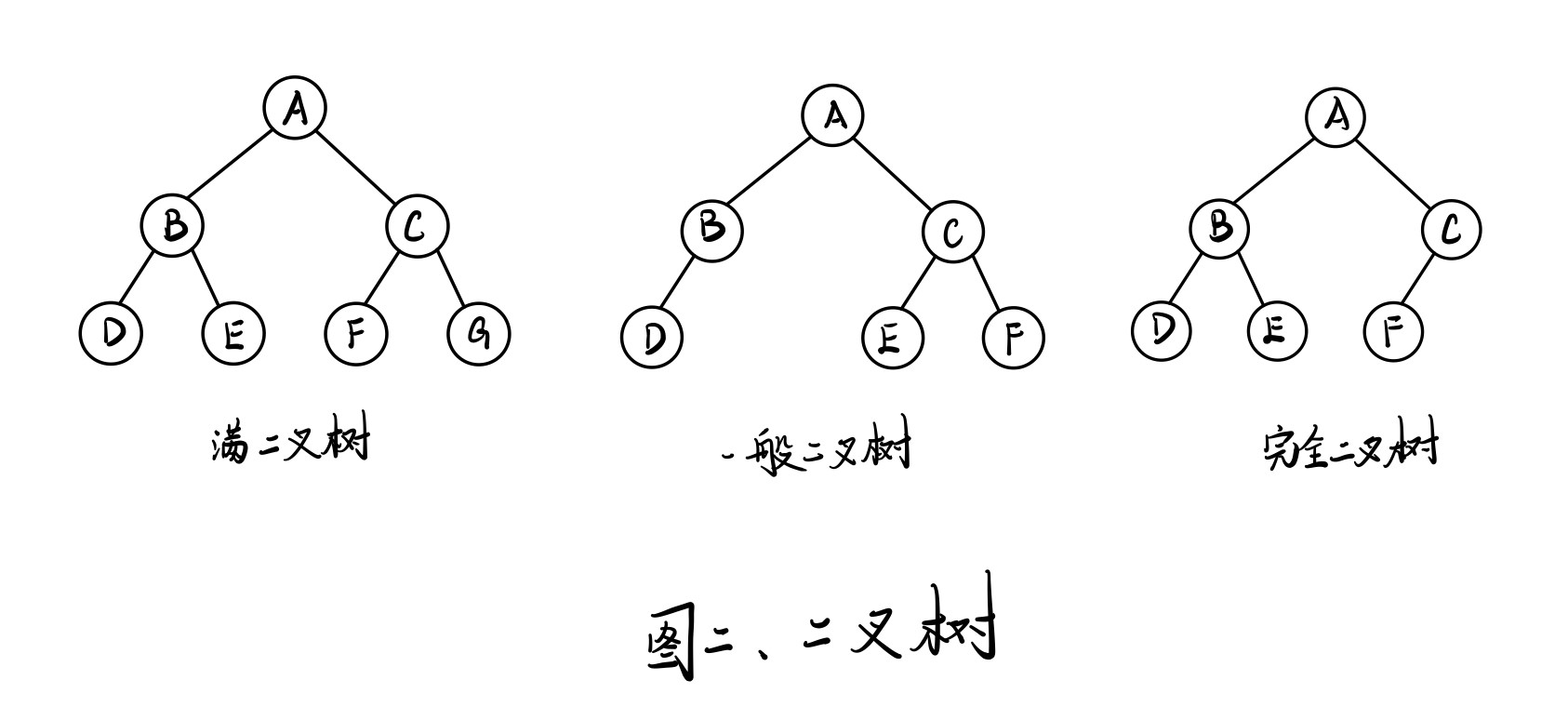
- 满二叉树:叶节点除外的所有节点均含有两个子树的树被称为满二叉树
- 国内的定义:树中每一层的节点树都到达最大值,外观上就像一个三角形
- 国外的定义:对于树中的任意节点,要么度数为0,要么度数为2
- 完全二叉树:如果对满二叉树的结点进行编号, 约定编号从根结点起, 自上而下, 自左而右。则深度为的, 有n个结点的二叉树, 当且仅当其每一个结点都与深度为k的满二叉树中编号从的结点一一对应时, 称之为完全二叉树。【说人话呢就是一棵树抛开最后一层不看,剩余部分满足一颗满二叉树的定义;并且最后一层的节点是从左到右紧密排好的】
- 哈夫曼树(最优二叉树):带权路径最短的二叉树称为哈夫曼树或最优二叉树
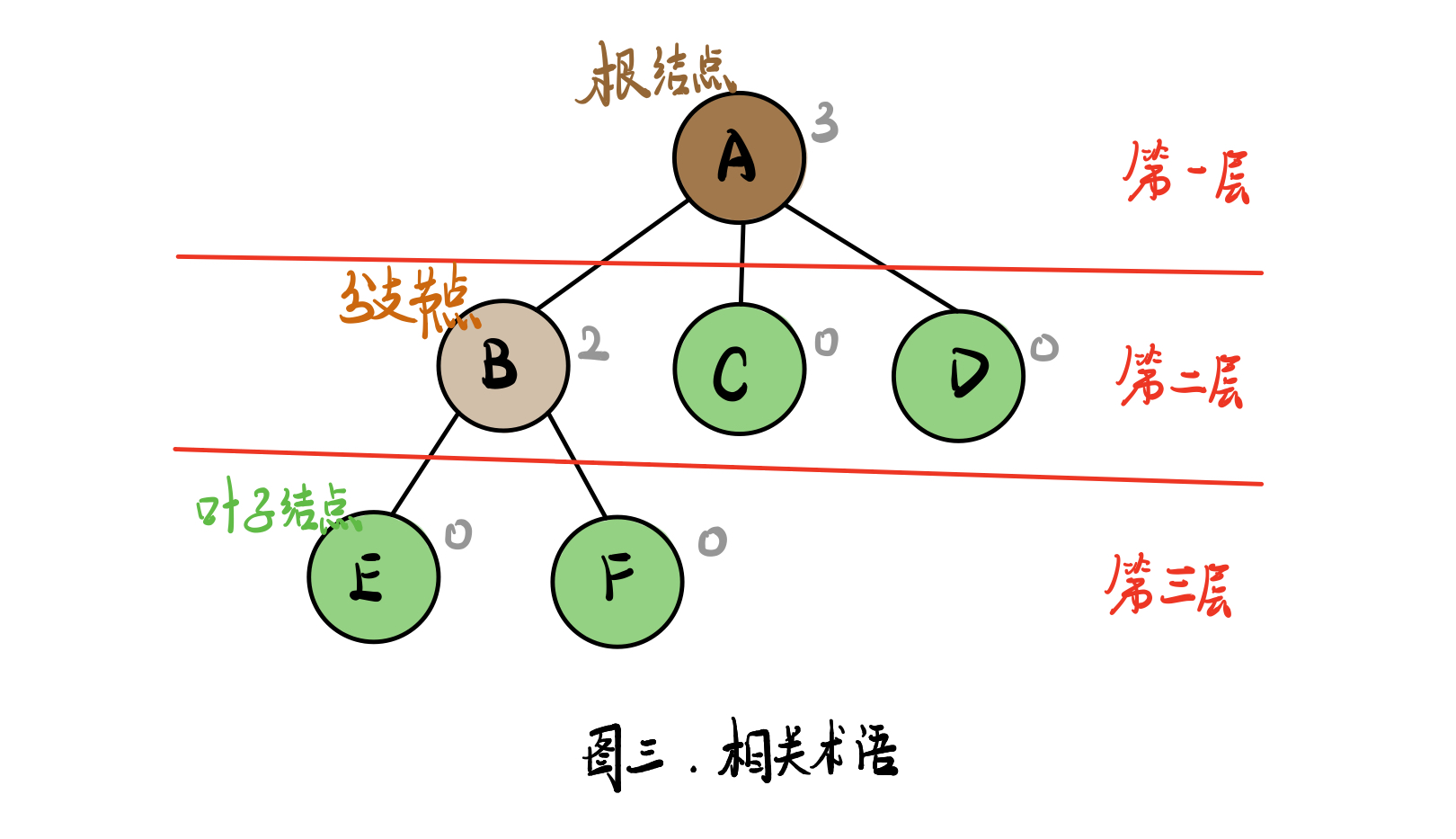
相关术语
- 结点:包含一个数据元素及若干指向子树分支的信息
- 结点的度:一个结点拥有子树的数目称为结点的度
- 叶子结点:也称为终端结点,没有子树的结点或者度为零的结点
- 分支结点:也称为非终端结点,度不为零的结点称为非终端结点
- 树的度:树中所有结点的度的最大值
- 结点的层次:从根结点开始,假设根结点为第1层,根结点的子节点为第2层,依此类推,如果某一个结点位于第L层,则其子节点位于第L+1层
- 树的深度:也称为树的高度,树中所有结点的层次最大值称为树的深度
- 权值: 边权、点权
二叉树的遍历
前、中、后 三序遍历,针对的是根节点的位置。根-左-右即前序遍历【所谓先遍历根节点,所以是前序】;左-根-右即中序遍历;左-右-根即后序遍历;而层序遍历则是按层数从低到高,从左到右的顺序遍历。
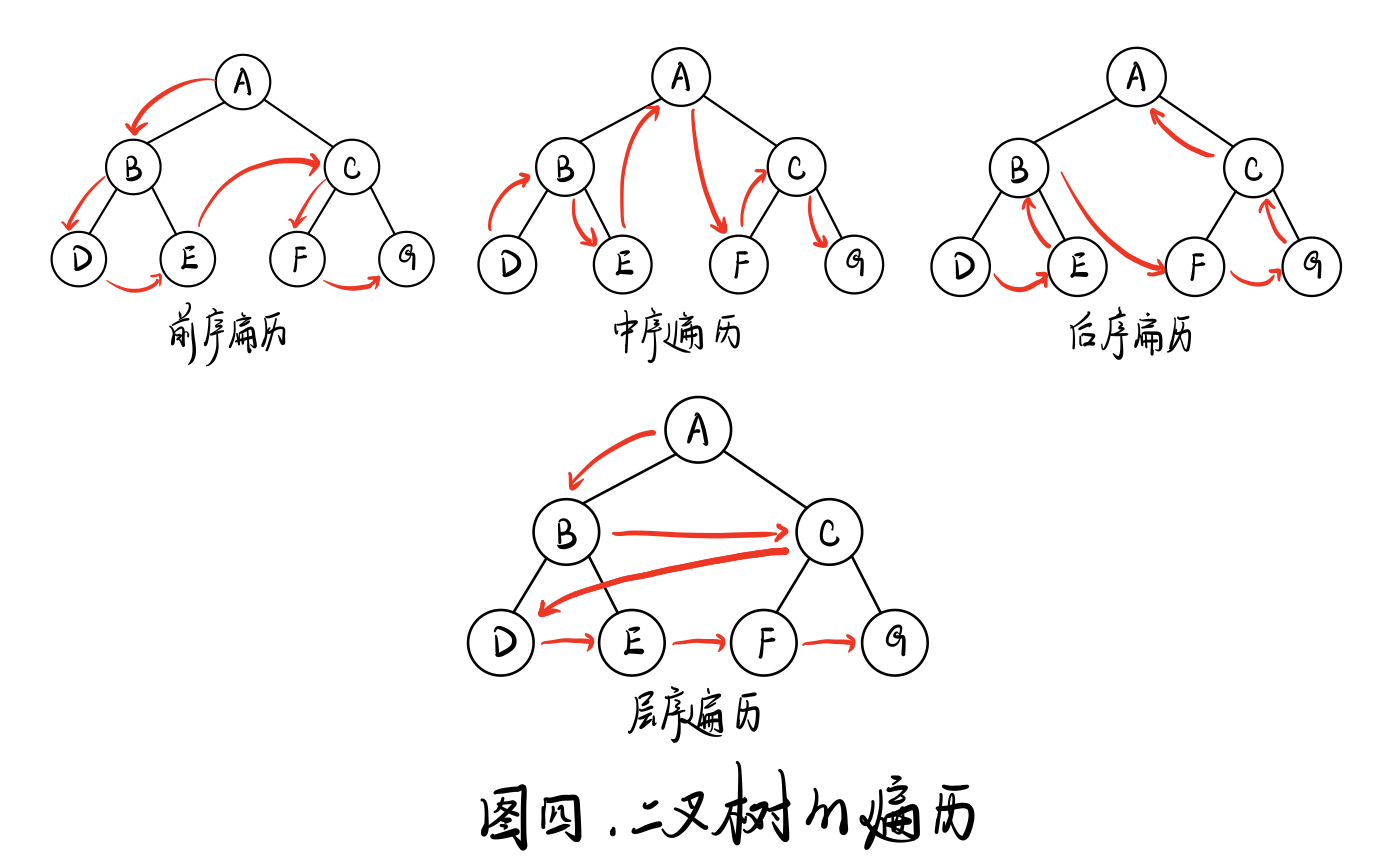
哦,还有一般的树的遍历:
1 |
|
【树形相关】的回顾
线段树
线段树是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。
- 建树
- 单点修改
- 区间修改
- 区间查询
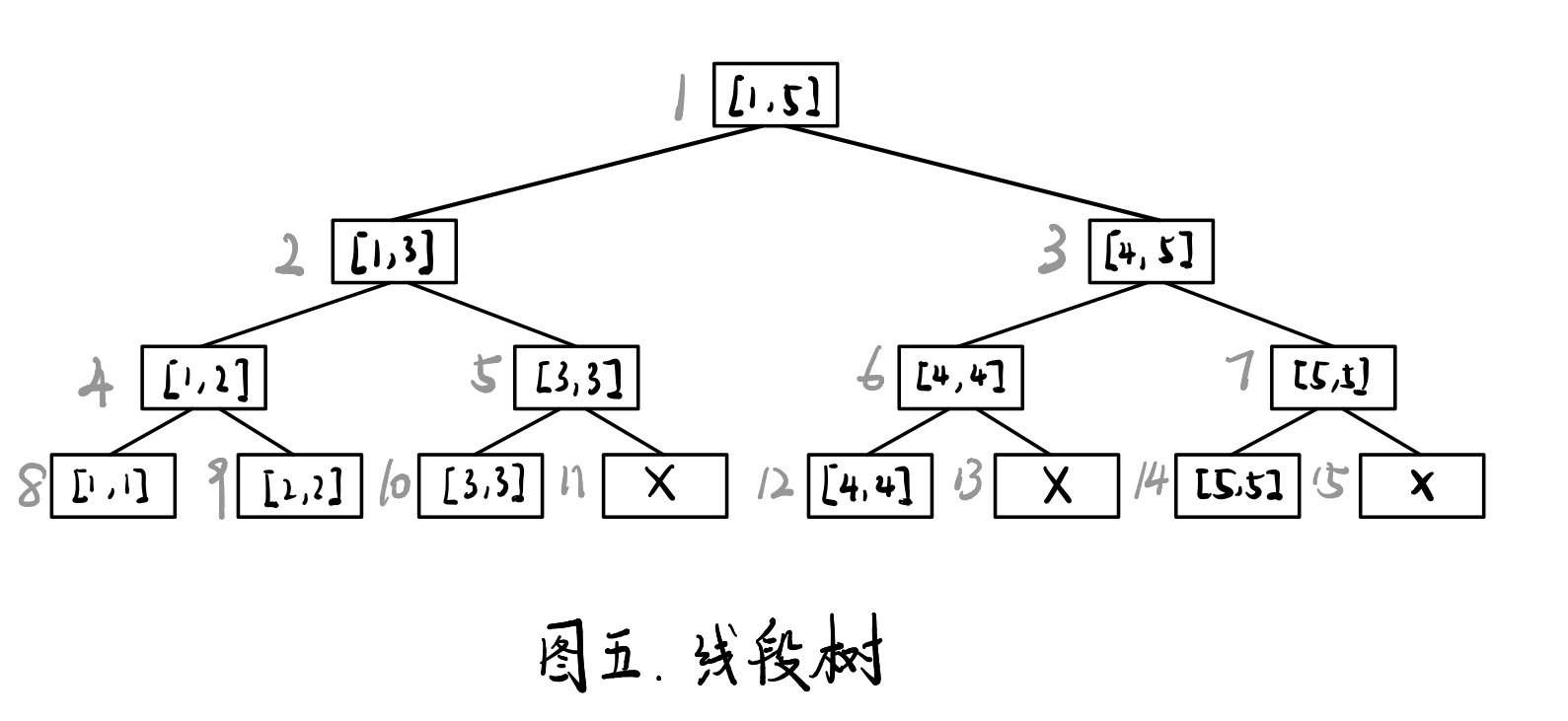
最小生成树
一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边。
- Prim算法
- Kruskal算法
- 次小生成树
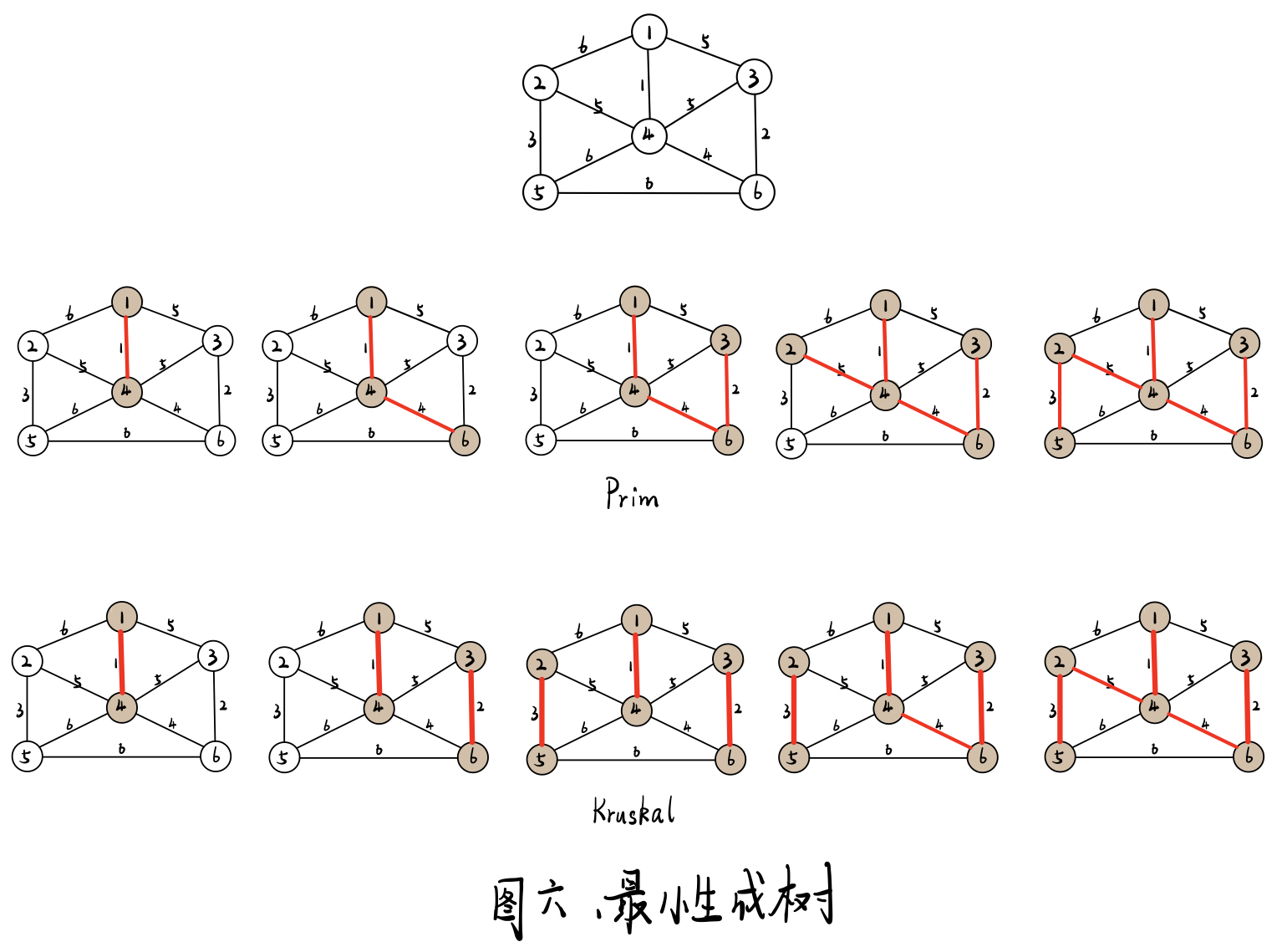
最近公共祖先
对于有根树T的两个结点u、v,最近公共祖先LCA(T,u,v)表示一个结点x,满足x是u和v的祖先且x的深度尽可能大。在这里,一个节点也可以是它自己的祖先。
- 在线倍增【略】
- 离线Tarjan【略】
今天的学习
树上差分
就是在树上进行差分,以起到优化复杂度的目的。主要作用是对树上的路径进行修改和查询操作,在修改多、查询少的情况下复杂度比较优秀。实际上,树上差分能够实现的操作,用线段树、树剖、LCT等等也可以实现,但它的优势在于实现简单,可以避免在考场上出现写题五分钟、调试两小时的情况
【差分】与【前缀和】
- 前缀和:数组中前个数的和
- 差分:数组中第个数和前一个数的差
| 原数组 | 9 | 4 | 7 | 5 | 9 |
|---|---|---|---|---|---|
| 前缀和 | 9 | 9 + 4 = 13 | 13 + 7 = 20 | 20 + 5 = 25 | 25 + 9 = 34 |
| 差分数组 | 9 | 4 - 9 = -5 | 7 - 4 = 3 | 5 - 7 = -2 | 9 - 5 = 4 |
| 前缀和的差分数组 | 9 | 13 - 9 = 4 | 20 - 13 = 7 | 25 - 20 = 5 | 34 - 25 = 9 |
| 差分数组的前缀和 | 9 | 9 - 5 = 4 | 4 + 3 = 7 | 7 - 2 = 5 | 5 + 4 = 9 |
原数组的前缀和的差分数组就是原数组,原数组的差分数组的前缀和还是原数组。 这就是差分与前缀和互为逆运算的原因,也是差分可以用来优化操作的原因。实际上,差分优化和前缀和优化原理类似,只是实现相反。前缀和优化常常对前缀和数组作差,差分优化也常常对差分数组求前缀和。
那就要问了,加和减也是互逆运算,乘和除也是互逆运算呢,不过都是一些很基础的运算而已。这里的前缀和和差分到底有什么运用呢。
例题:有一个区间的数组。每次操作可以对某个区间上的所有数字。若干次操作之后询问的值。
一看区间修改加查询,可能就有些人马上会反应到用【线段树】来做了。前文就有讲到,差分应用于修改多、查询少的题目,对比线段树等算法的优势就在于实现简单。
对于原数组,查询无非就是,但是修改需要暴力对整个区间所有的数都进行修改。时间复杂度【假设有m次修改,每次修改整个区间】
假设是数组的前缀和,题目中求转换过来其实就是。但是实现区间修改,本质上还是要暴力去修改每一个相关的,时间复杂度上对比原先没有改变。
再看差分数组。根据性质来看,想要从差分数组得到原数组,那么在查询之前就需要对差分数组进行求前缀和,时间复杂度,貌似效率还变低了,上当了。反观修改操作,因为差分是原数组的后一个数减去前一个数,如果在某次修改操作中,区间同时增加或减少了一定值,那么差分数组在区间上的值应该不受影响。所以一次区间修改只需要针对进行修改即可,时间复杂度。总体上看,时间复杂度优化到了
比如对区间
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 原数组 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 差分数组 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 修改 | 0 | +3 | +3 | +3 | +3 | +3 | 0 | 0 | 0 |
| 修改以后的原数组 | 1 | 4 | 4 | 4 | 4 | 4 | 1 | 1 | 1 |
| 修改以后的差分数组 | 1 | 3 | 0 | 0 | 0 | 0 | -3 | 0 | 0 |
树上差分
理解完差分以后,我们需要将差分试着应用到树上,这才是我们今天的课题。那对于一棵有可能有很多分支的树,我们的差分也只能是对于某一条分支的。【不再啰嗦,直接上图,只要记住两种差分的区别然后能过应用即可】
- 从叶子节点向根节点的方向进行计算差分【为什么】
- 需要计算两点的LCA【倍增、Tarjan】
点的差分
- 对节点u到节点v路径上的所有节点的权值+c
w[u]+=c, w[v]+=c, w[lca{u,v}]-=c, w[fa[lca{u,v}]]-=c;
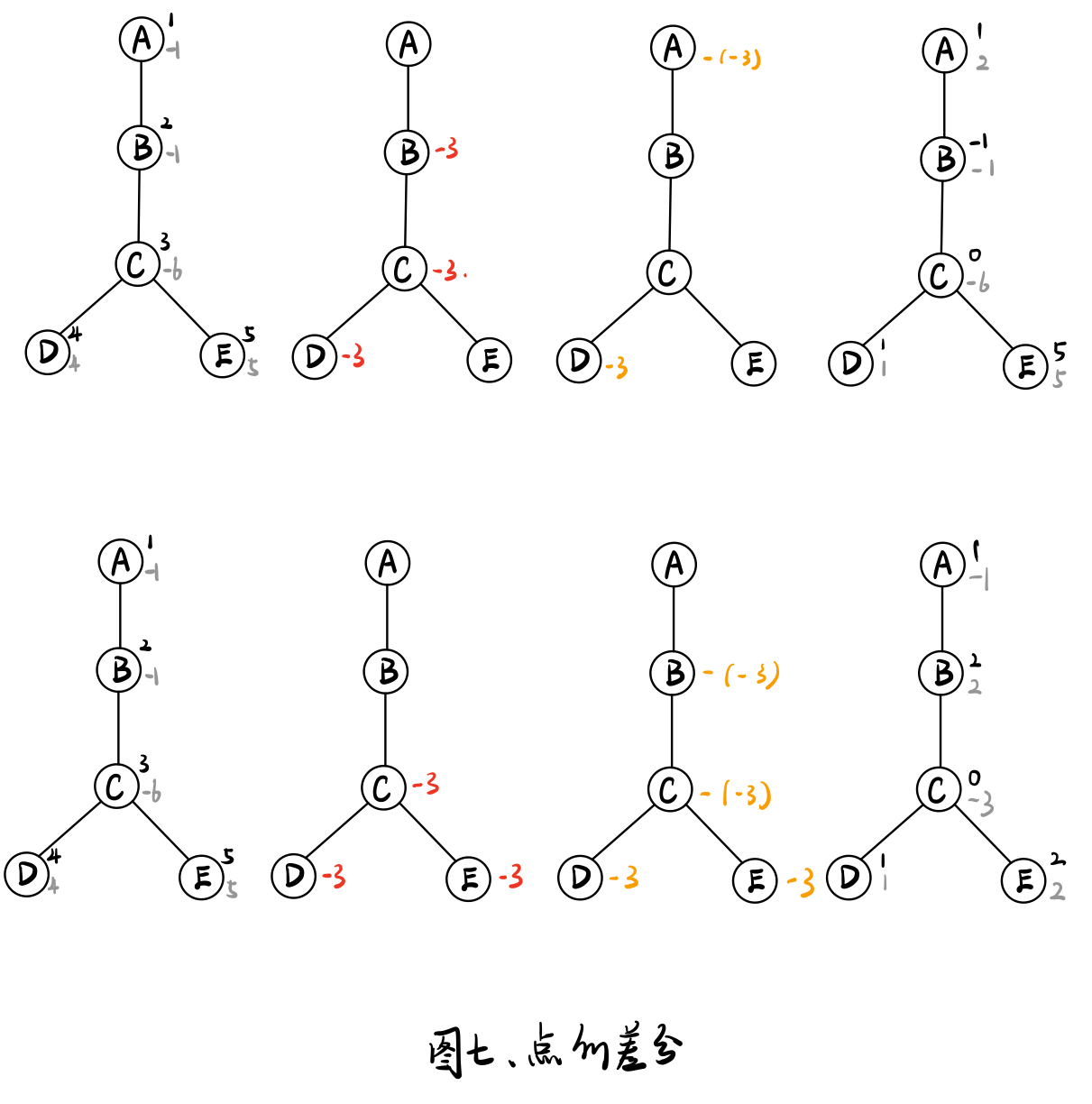
边的差分
- 【假设u是v的父节点】将u与v边上的权值记到点v上
- 对节点u到节点v路径上所有的边的权值+c
w[u]+=c, w[v]+=c, w[lca{u,v}]-=2*c;
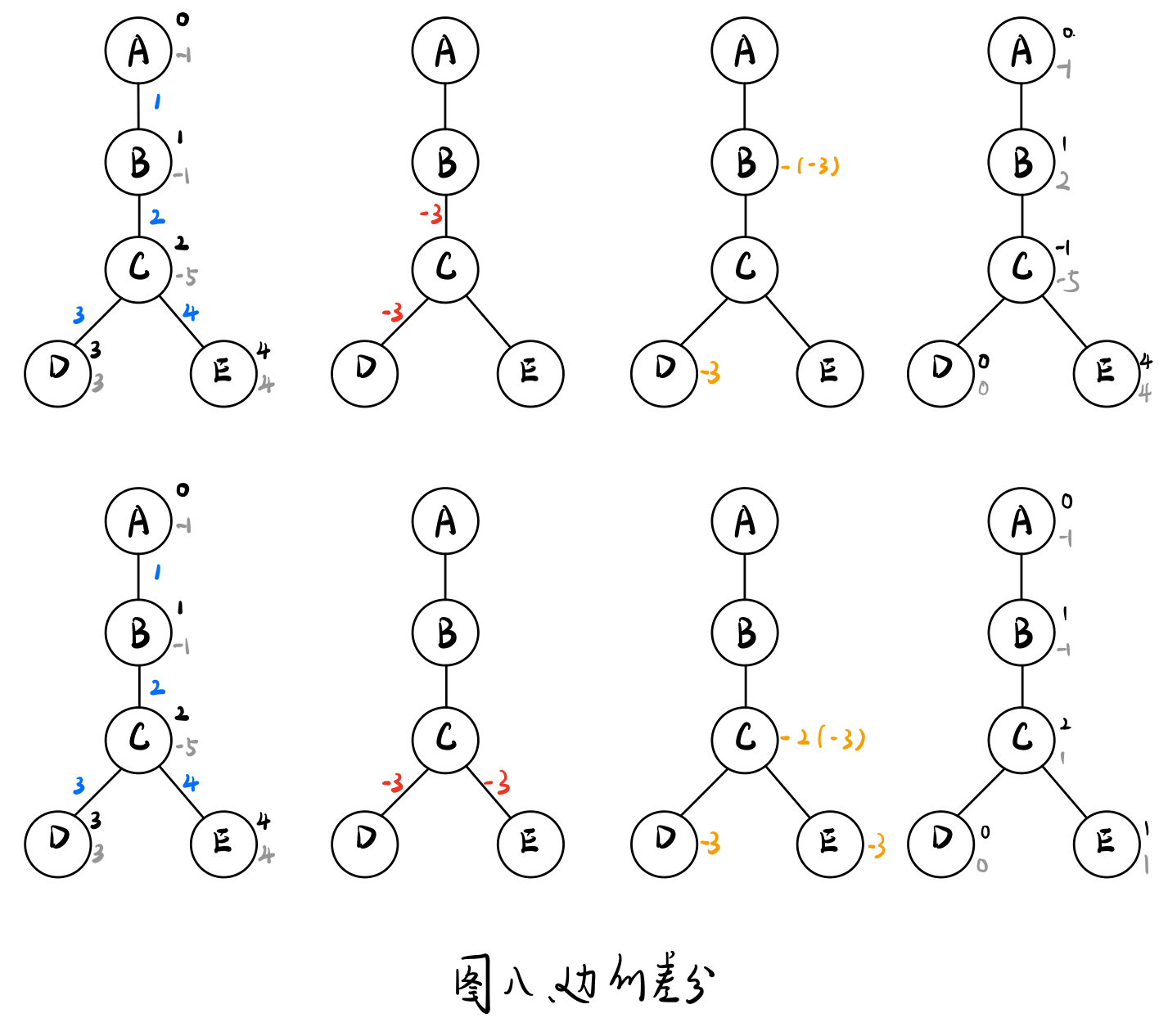
树的重心
定义: 树的重心也叫树的质心。对于一棵树n个节点的无根树,找到一个点,其所有的子树中最大的子树节点数最少,那么这个点就是这棵树的重心
性质:
- 树中所有点到某个点的距离和中,到重心的距离和是最小的,如果有两个重心,他们的距离和一样。
- 把两棵树通过一条边相连,新的树的重心在原来两棵树重心的连线上。
- 一棵树添加或者删除一个节点,树的重心最多只移动一条边的位置。
- 一棵树最多有两个重心,且相邻。
算法:
【算法思路】
- 枚举每个节点作为根节点,去计算这个根节点下【【每个孩子节点作为根】的子树】的节点个数。
- 找到某个节点作为根节点时,它的最大子树节点最少,即为重心。
【虽然但是】
- 『枚举每个节点作为根节点』不可以也没必要,
那只是我陈述理论的时候方便理解而已。实际算法过程只需要假设一个节点作为根节点,然后随便DFS一下就可以了。 - DFS过程中去计算子树节点个数的时候,某一节点的孩子节点应该还包括它的【父节点】。听上去有些自相矛盾,但因为一开始的时候也只是随便假设了一个根节点,算是一个假根,所以一个节点的父节点也算得上是这个节点的【潜在孩子节点】。
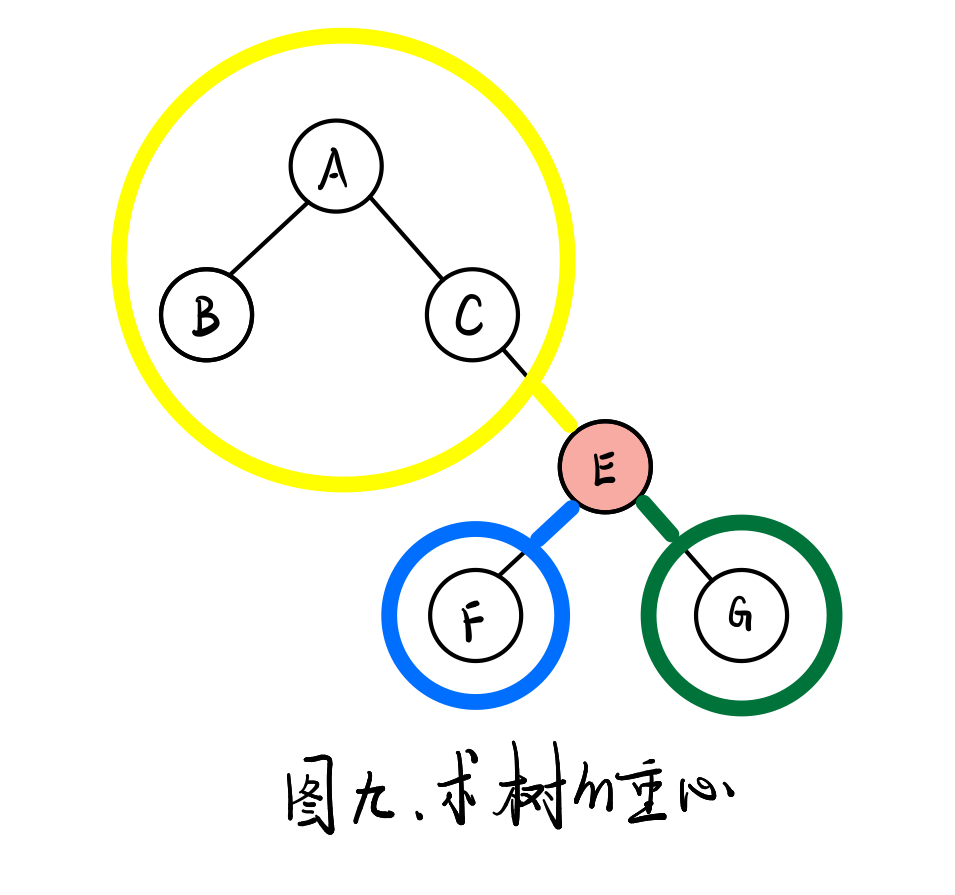
- 定义
sz[i]表示节点为根的子树的节点个数。 - 定义
dp[i]表示节点为父节点的【所有孩子节点为根】的最大子树节点个数。
在吗,看看代码
1 | void DFS (int u, int fa) { |
树的直径
定义: 树中所有最短路径距离的最大值即为树的直径
什么是距离?对于一棵带边权的树,距离就是边权;反之没有边权的树,相连接的两点的距离就默认为1。
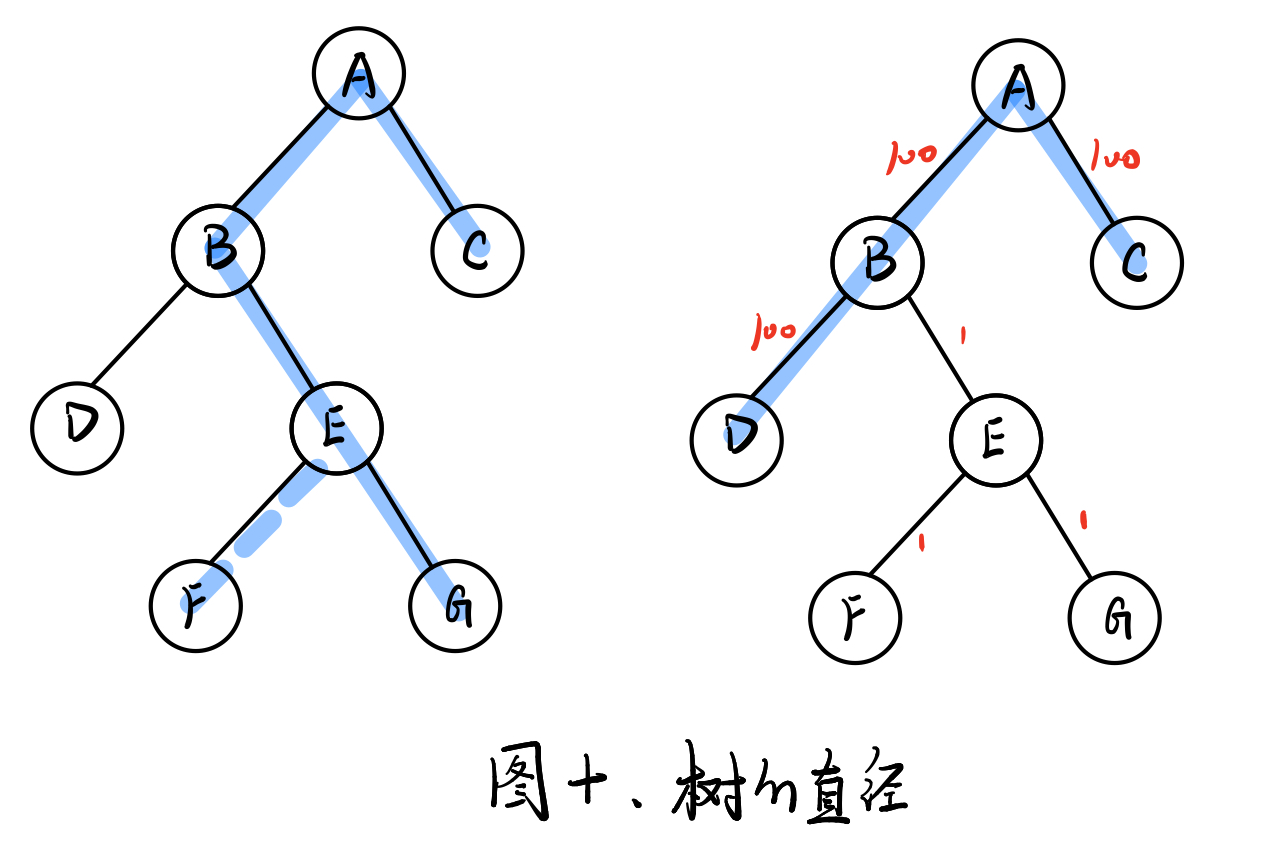
算法: 选择任意一点开始DFS,找到离这个点最远的点;再从点开始DFS,找到离点最远的点。最后点到点的距离就是这棵树的直径。
出来给我看下代码
1 | void DFS (int u, int fa, int dis) { |
树的中心
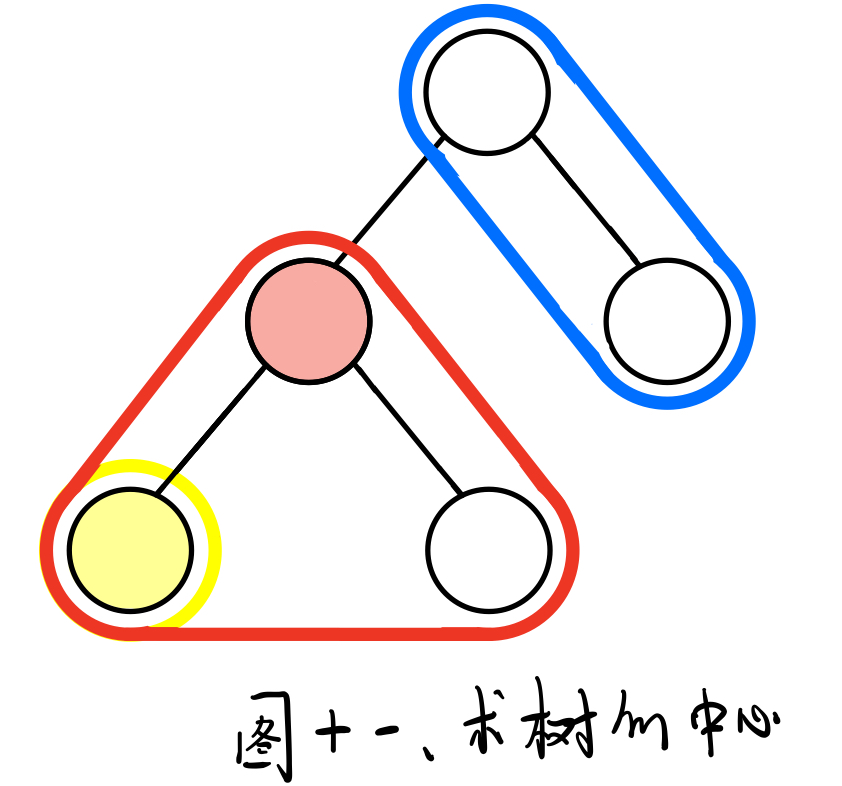
定义: 以树的中心为整棵树的根时,从该根到每个叶子节点的最长路径最短。区别于树的重心【重心下的最大子树节点数最小】。
算法一:直径上暴力
根据定义,废话, 树的中心一定在树的直径上,所以在找到直径的两端点之后,离这两端点的最远距离最小【有点不说人话,总之就应该是最近的】的就是中心。
在,代码,懂?
1 | // 我是代码: |
算法二:树形DP
求什么?
- 树的中心,最长距离最小。
- 那就定义
dp[u]表示到节点u的最长距离。
怎么求?
要想完成状态转移,势必需要通过DFS遍历这棵树。
先看看DFS的特点
1 |
|
如果把握好递归函数里的语句顺序,我们可以实现【把孩子节点的信息传递给父节点】,或是【把父节点的信息传递给孩子节点】。
但是,这两步操作不能写在同一个函数里。
孩子节点的信息收集好了才能正确传递给父节点吧?
父节点的信息收集好了才能正确传递给孩子节点吧?

求某根节点在子树中的最长距离
1 | void DFS (int u, int fa) { |
利用刚计算好的dp向上更新
1 | void DFS (int u, int fa) { |
- 假设我们已经求出全部子树中,根节点的最长距离。然后利用这一信息,向上更新。
- 整棵树剔除红色部分之后,根节点在子树中的最长距离信息,可以用来更新红节点向上的最长距离
于是又多了一个问题,好好的一棵树,我要怎么忽略某个部分。
一个父节点的众多孩子节点中,对于孩子节点V,其实只有两种关系,是V本身,非V节点。
所以我们在计算某根节点在子树中的最长距离时,顺便就求一下次长距离就好了。
在跟新某孩子节点向上的最长距离时,判断孩子节点的位置,然后选择最长距离或者次长距离即可。
直接上代码不行么
1 | void dfs (int u, int fa) { |

结尾总结
